
Pytorch - Simple Linear Regression
- 6 minsThis is the fourth tutorial of the Explained! series and the start of the Pytorch tutorials.
I will be cataloging all the work I do with regards to PyLibraries and will share it here or on my Github.
That being said, Dive in!
# Necessary imports
import torch
import numpy as np
import matplotlib.pyplot as plt
# Create the sample dataset
X = np.array([1.0, 20.4, 30.5, 7.5, 9.9,
100.9, 200.1, 45.1, 150.1, 7.0,
29.4, 31.5, 157.3, 10.9, 120.6,
16.9, 201.1, 21.1, 300.1, 21.0,
120.4, 230.5, 37.5, 49.9, 230.0,
109.9, 121.1, 145.1, 157.1, 17.0,
219.4, 131.5, 187.3, 210.9, 290.6,
126.9, 71.1, 91.1, 19.1, 100.0])
X_train = []
# normalize each value
for i in X:
X_train.append([i/100])
X_train = np.array(X_train)
y_train = np.array([i*0.175 + 0.4 for i in X_train]) # bias should be 0.4 and w=0.175
# Check the shape of the data to be sure
print(X_train.shape)
print(y_train.shape)
(40, 1)
(40, 1)
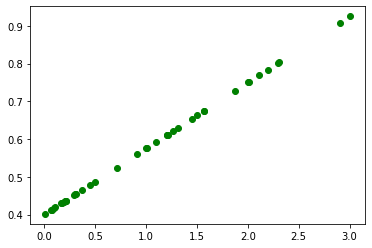
# Visualize the data
plt.scatter(X_train, y_train, c="green", label="Original Data")
plt.show()
# Create the torch tensors
X = torch.from_numpy(X_train)
y = torch.from_numpy(y_train)
print(X.shape)
print(y.shape)
torch.Size([40, 1])
torch.Size([40, 1])
# Define the parameters needed
input_size = 1
hidden_layers = 1
outputs = 1
learning_rate = 0.001
num_epochs = 150
# Create the first weight tensor
w1 = torch.rand(input_size, hidden_layers, requires_grad=True)
print(w1.shape)
torch.Size([1, 1])
b1 = torch.rand(hidden_layers, outputs, requires_grad=True)
print(b1.shape)
torch.Size([1, 1])
for i in range(1, num_epochs):
# y = wx + b - one forward pass
y_pred = X.mm(w1.double()).clamp(min=0).add(b1.double())
# Here the `.clamp(min=0)` works as the ReLu actiation function
# calculate the loss
loss = (y-y_pred).pow(2).sum()
if i % 25==0:
print("Epoch : ", i, "\t Loss :", loss)
# backpropogation
loss.backward()
with torch.no_grad():
# update the weights and biases
w1 -= (learning_rate * w1.grad)
b1 -= (learning_rate * b1.grad)
# set the gradients to 0
w1.grad.zero_()
b1.grad.zero_()
Epoch : 25 Loss : tensor(0.0021, dtype=torch.float64, grad_fn=<SumBackward0>)
Epoch : 50 Loss : tensor(0.0004, dtype=torch.float64, grad_fn=<SumBackward0>)
Epoch : 75 Loss : tensor(0.0001, dtype=torch.float64, grad_fn=<SumBackward0>)
Epoch : 100 Loss : tensor(4.1570e-05, dtype=torch.float64, grad_fn=<SumBackward0>)
Epoch : 125 Loss : tensor(1.3125e-05, dtype=torch.float64, grad_fn=<SumBackward0>)
print(w1)
print(b1)
tensor([[0.1753]], requires_grad=True)
tensor([[0.3995]], requires_grad=True)
That’s pretty close to the actual values we used.
You can try running with more iterations if you want to see if you ever get the actual values!
# Let's visualize the output
plt.scatter(X, y, c="green", s=150, label="Original Data")
plt.plot(X, y_pred.detach().numpy(), label="Fitted Line")
plt.legend()
plt.show()
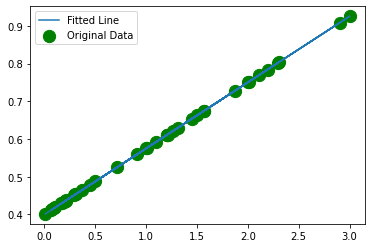
As you can clearly see the line fits very well with the data.
This is a simple one neuron network that simply performs linear regression.
You might never use this in practice but the idea is to understand the concept!
Find more at my Github repository Explained.
Show some ![]() by
by ![]() ing it.
ing it.